Lecture 12

The Binomial Probability Distribution

Section 5.2 The Binomial Probability Distribution

A binomial experiment is one that has these five characteristics:

1. The experiment consists of n identical trials
2. Each trial results in one of two outcomes. Success (S) and Failure (F)
3. Probability of success is always equal to p and probability of failure is \(1 - p = q\).
4. The trials are independent
5. The binomial random variable x is the number of successes in n trials.

• If you select 1000 people and ask them if they like basketball - is this a binomial experiment?

• If you have 20 balls, 10 red and 10 blue - and you pick 4. Is the number of red balls that you pick the result of a binomial experiment?

The Binomial Probability Distribution

\[ P(x = k) = C^n_k p^k q^{n-k} = \frac{n!}{k! (n-k)!} p^k q^{n-k} \]

\[ \begin{aligned} \mu &= np \\ \sigma^2 &= npq \\ \sigma & = \sqrt{npq} \end{aligned} \]

Example 5.7

Let’s say a basketball player can make free throws with a probability of 80%. If she shoots 10 shots, what’s the probability that she makes exactly 8.

if p = .8 and n = 10, find P(x = 8)

1. What is one way that we can observe 8 successes and 2 failures?
2. What’s the probability of that happening?
3. Can we observed 8 successes and 2 failures any other way?

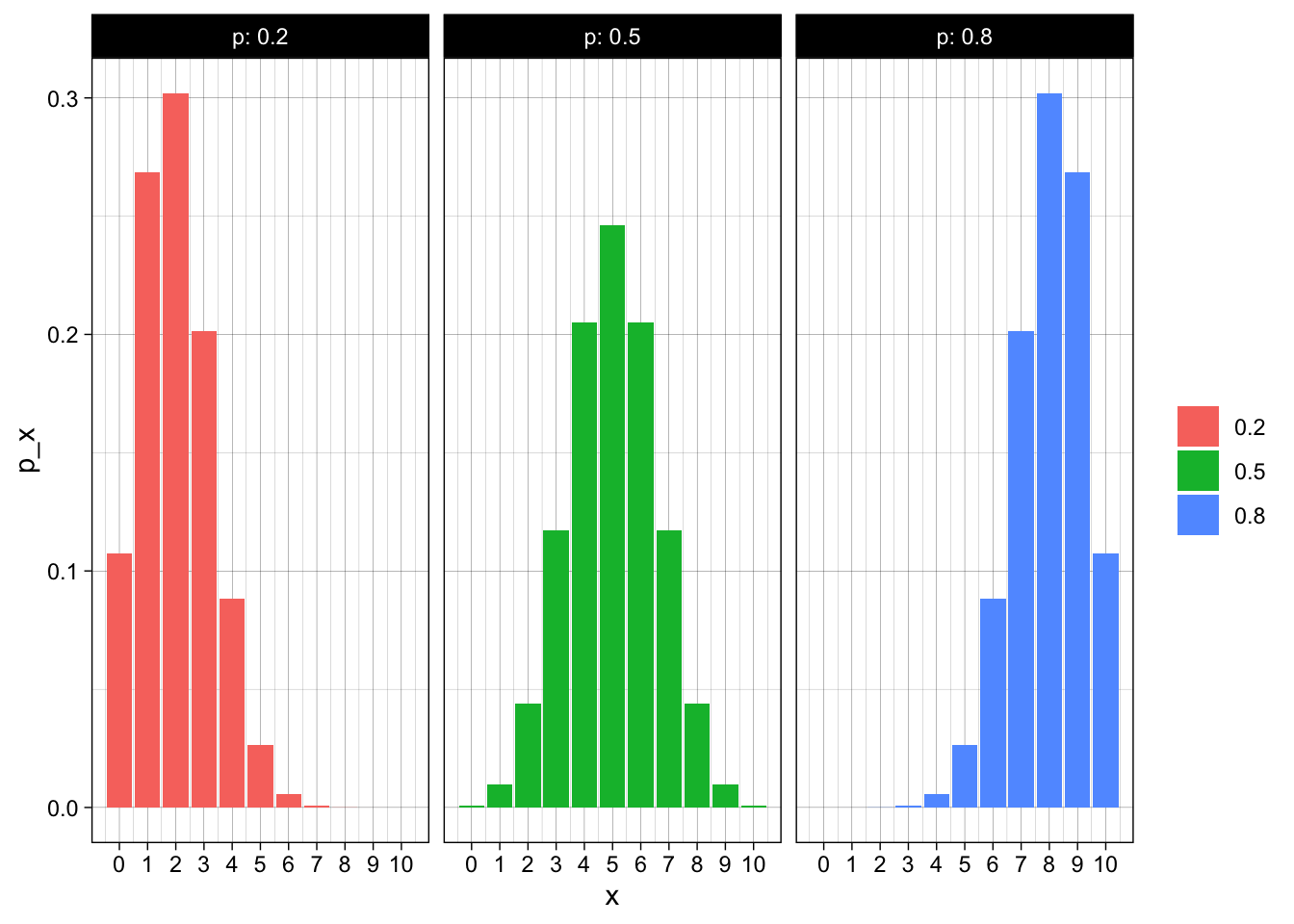
Histograms for different values of p

x	0.2	0.5	0.8
0	0.107	0.001	0.000
1	0.268	0.010	0.000
2	0.302	0.044	0.000
3	0.201	0.117	0.001
4	0.088	0.205	0.006
5	0.026	0.246	0.026
6	0.006	0.205	0.088
7	0.001	0.117	0.201
8	0.000	0.044	0.302
9	0.000	0.010	0.268
10	0.000	0.001	0.107

What if I now ask - what is the probability of making at least 6? (\(P(x \ge 6)\))

What about \(P(x \lt 6)\)?

Cumulative Binomial Probabilities

\[ P(\le 3) = p(0) + p(1) + p(2) + p(3) \]

x	0.2	0.5	0.8
0	0.107	0.001	0.000
1	0.376	0.011	0.000
2	0.678	0.055	0.000
3	0.879	0.172	0.001
4	0.967	0.377	0.006
5	0.994	0.623	0.033
6	0.999	0.828	0.121
7	1.000	0.945	0.322
8	1.000	0.989	0.624
9	1.000	0.999	0.893
10	1.000	1.000	1.000

Let’s look at the column where p = 0.2, how do you find

• \(P(x \le 2)\)?
• \(P(x \gt 2)\)?
• \(P(x = 2)\)?
• \(P( 3 \le x \lt 6)\)?

See the table 1 in appendix I (pg 682)

Use the table for n = 5, p = 0.6.

Find probability of exactly 3 successes

Find probability of three or more successes

Example 5.11

Let’s assume someone is interested in testing if vitamin C help prevent the common cold during the winter. Let’s assume that the probability of making it through the winter without experiencing the common cold = 0.5.

You give 10 people vitamin C and only 2 get sick. What is the probability that only 2 or fewer folks get sick if the probability of getting sick is 0.5?

Homework

[1] "5.2.11-15, 5.2.39, 5.2.51, 5.2.55"

Answers: Section 5.2