Homework Chapter 5

Section 1

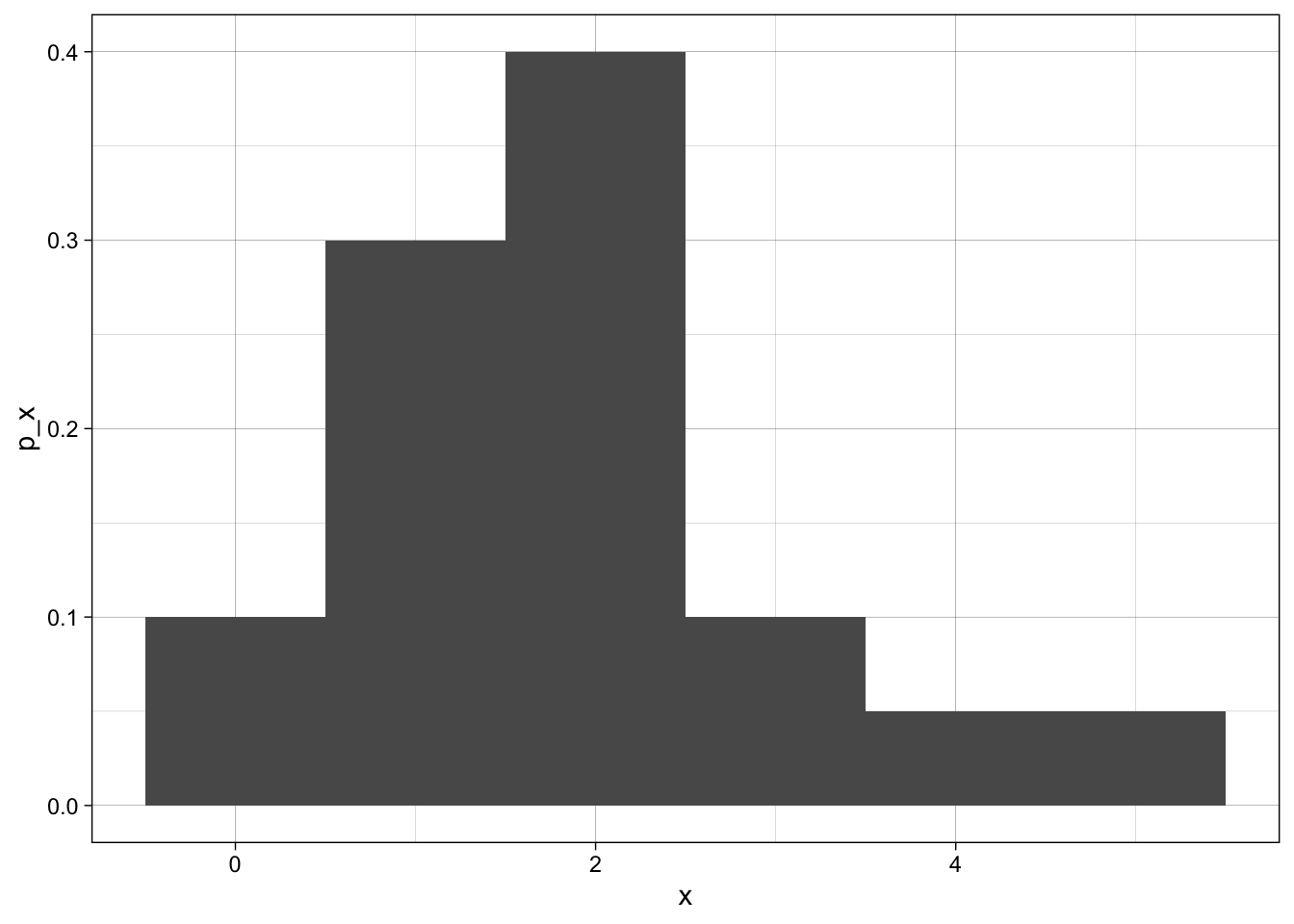
\[ p(4) = 1 - (.1 + .3 + .4 + .1 + .05) = .05 \]

x	p_x	x * p_x	x - mu	(x - mu)^2*p_x
0	0.10	0.00	-1.85	0.342
1	0.30	0.30	-0.85	0.217
2	0.40	0.80	0.15	0.009
3	0.10	0.30	1.15	0.132
4	0.05	0.20	2.15	0.231
5	0.05	0.25	3.15	0.496

Mean:

[1] 1.85

Variance:

[1] 1.427

Standard Deviation:

[1] 1.194571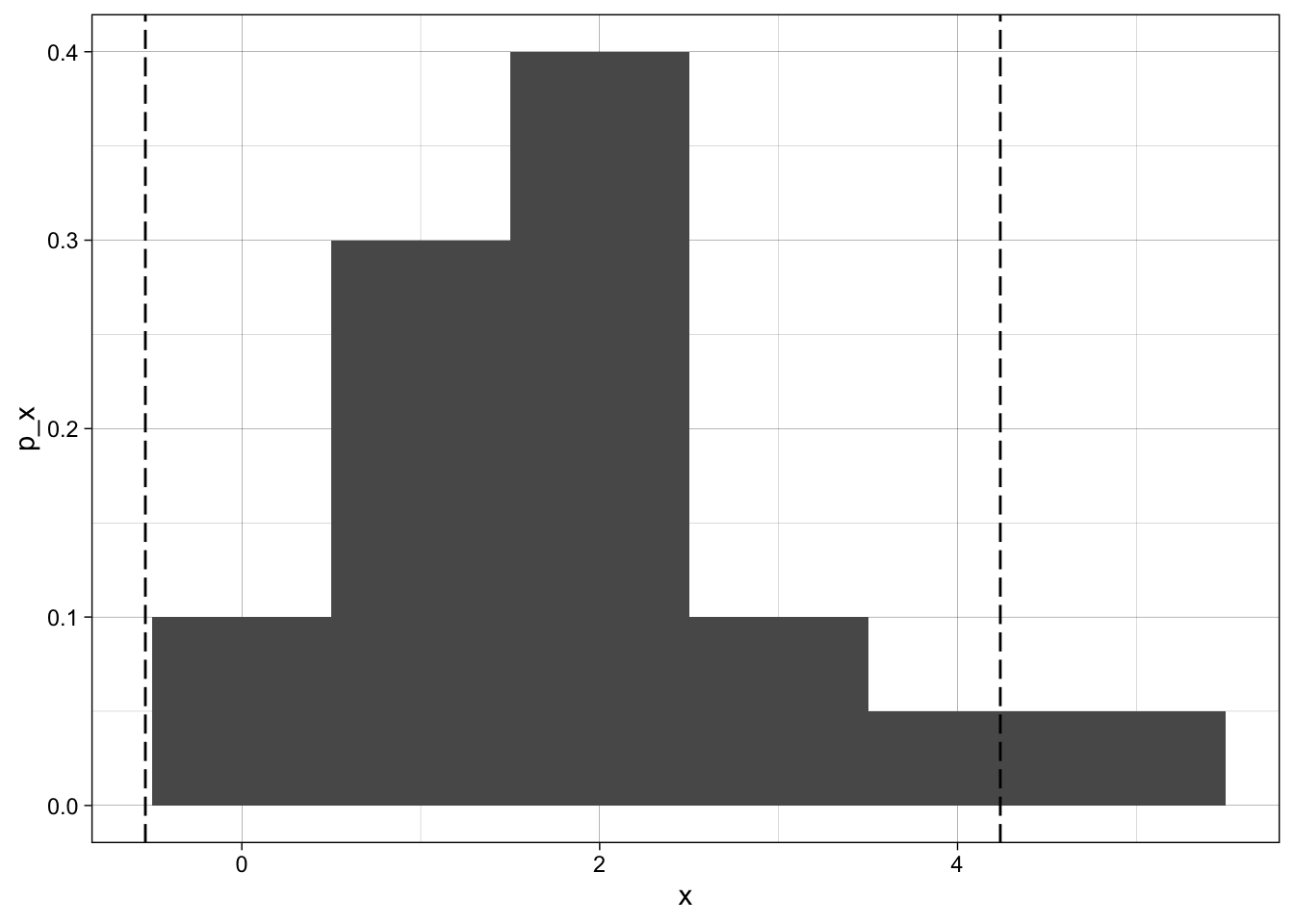

This interval contains approximately 95% of the data since the data is relatively mound shaped. Interval:

[1] -0.54  4.24

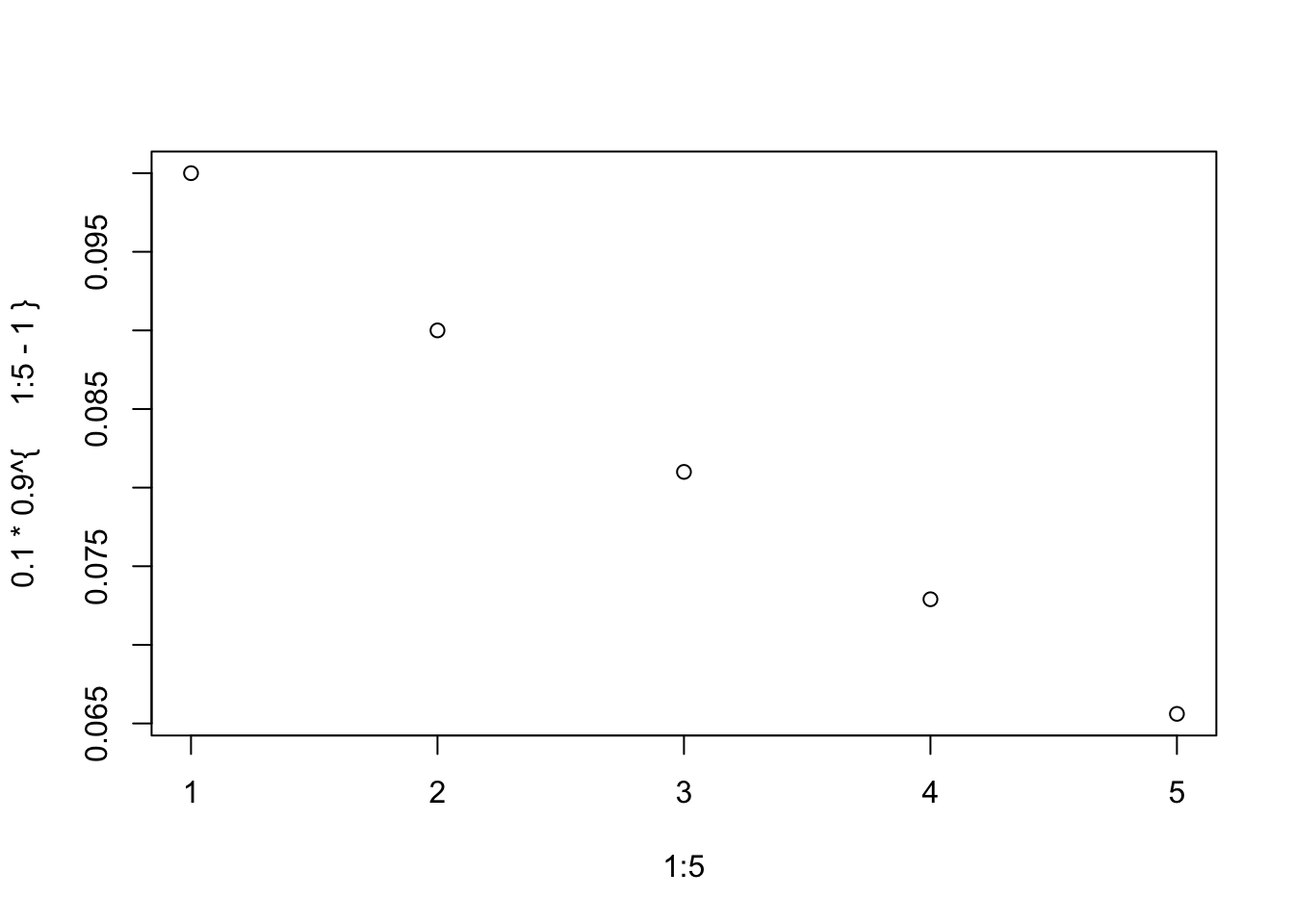
Probability of oil at any well \(P(O) = .1\) Probability of no oil is therefore \(P(O^c) = .9\) Probability that your first well has oil:

\[ p(1) = .1 \]

If you only hit on the second try then that means you missed on the first well and hit on the second.

\[ p(2) = P(O^c) * P(O) = .09 \]

You can keep adding ‘missed wells’ with 3, etc.

\[ p(3) = P(O^c) * P(O^c) * P(O) = 0.081 \]

\[ p(n) = .1 \times .9^{n - 1} \]

[1] 7.9

[1] 2.174856

interval:

[1]  3.55 12.25

You can estimate it as about the data that runs between 4 and 11: Approximately:

[1] 0.97

Very similary to the expected 95%

\[ P(x = 4) = .27 \]

\[ P(x \le 1) = .0625 \]

\[ P(x \gt 1) = 1 - P(x \le 1) = .9375 \]

\[ \mu = 7*.5 = 3.5 \]

\[ \sigma = \sqrt(7 * .5 * .5) = 1.32 \]

\[ P(x = k) = C^3_k .5^k (1 - .5)^{3 -k} = C^3_k .5^3 \]

\[ \mu = .5 *3 = 1.5 \]

\[ \sigma = \sqrt(3 * .5 * .5) = .87 \]

Intervals 1-sigma

[1] 0.63 2.37

Probability interval is about 75% of data, Emperical rule says 68%, Tchebysheff’s says 0%

Intervals 2-sigma

[1] -0.24  3.24

Probability interval is 100% of data, Emperical rule says 95%, Tchebysheff’s says 75%

p = .1, n = 25 - see table 1 in Appendix I

\[ P(x = 1) = C^8_1 .23^1 (1 - .23)^{7} = .295 \]

\[ 1 - .42 = .58 \]