Lecture 19
The Sampling Distribution of the Sample Proportion
Section 7.5 the Sampling Distribution of the Sample Proportion
Can you estimate the true population proportion p from a sample?
- Binomial distribution has mean of what?
- What about standard deviation?
Properties of the Sampling Dsitribution of the Sample Proportion of \(\hat p\)
- If a random sample of n observations is selected from a binomial population with parameter p, then the sampling distribution of the sample proportion
\[ \hat p = \frac x n \]
will have a mean
\[ p \]
and a standard deviation
\[ \text{SE}(\hat p) = \sqrt{ \frac {pq}{n}} \]
When sample size on is large, the sampling distribution of \(\hat p\) can be approximated by a normal distribution. The approximation will be adequate if \(np > 5\) and \(nq > 5\).
Example 7.10
- 500 parents asked about the importance of sports for boys and girls. Of the parents interviewed, 60% agreed that boys and girls should have equal opportunities to participate in sports. Describe the sampling distribution of the sample proportion \(\hat p\) of parents who agree that boys and girls should have equal opportunities.
\[ \text{SE}(\hat p) = \sqrt{ \frac {pq}{n}} \approx \sqrt{ \frac {\hat p \hat q}{n}} = \sqrt{ \frac {.6 * .4}{500}} = .022 \]
Create 95% Interval
95% of the time, \(\hat p\) will fall within 2SE \(\approx .044\) of the unknown value of \(p\)
This is the first time we have estimated a parameter from the data - and estimated the uncertainty around the estimate.
We have generally reversed the situation and assumed a population proportion \(p\) and calculated the probability of how likely or unlikely a sample proportion \(\hat p\) might be.
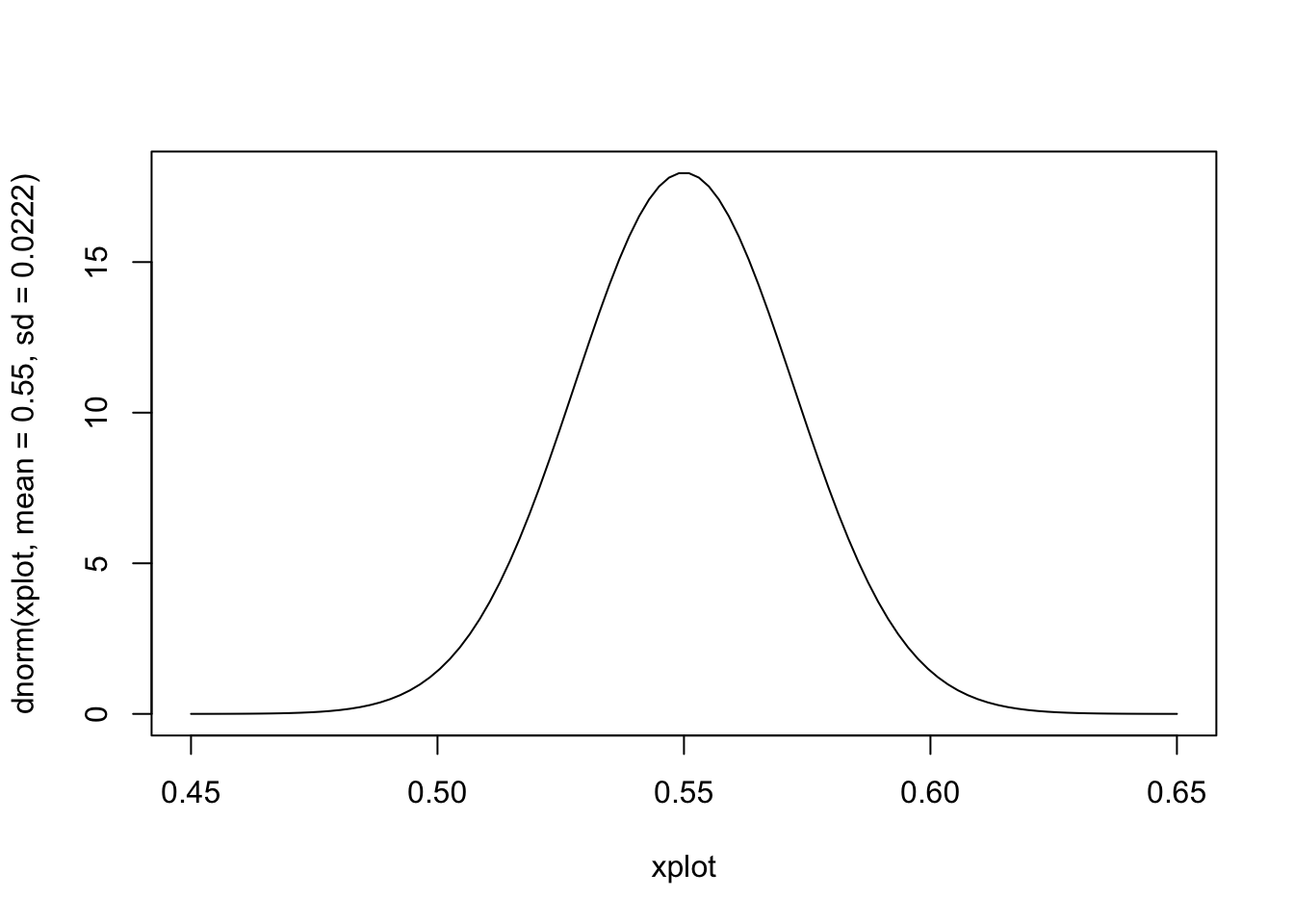
Example 7.11
Suppose someone claims that the proportion \(p\) of parents in the population is actually .55. What is the probability of observing a sample proportion as large as or larger than \(\hat p = .6\)
\[ \text{SE}(\hat p) = \sqrt{ \frac {pq}{n}} = \sqrt{ \frac {.55 * .45}{500}} = .0222 \]
\[ z = \frac{\hat p - p}{\sqrt{pq/n}} = \frac{.6 - .55}{.0222} = 2.25 \]
\[ P(\hat p > .6) \approx P(z > 2.25) = 1 - .9878 = .0122 \]
With continuity correction:
\[ z_1 = \frac{(.6 - .5/500) - .55}{.0222} = 2.20 \]
Midterm 02 Review
All Homework + Quiz questions and:
- Section 5.2: 30, 38, 44, 46
- Section 6.1: 5-8, 17, 20
- Section 6.2: 49-52, 56, 59, 61
- Section 6.3: 17, 19, 24, 28
- Section 7.3: 23, 25, 29, 32
- Section 7.5: 26, 27, 28, 33