Lecture 8/9

Rules for Calculating Probabilities

Published

September 21, 2023

Section 4.4 Rules for Calculating Probabilities

Let A and B be two events defined in the sample space S

  • union - \(A \cup B\) - is the event that either A or B or both occur

  • intersection - \(A \cap B\) - both A and B occur

  • complement - \(A^c\) is the event that A does not occur

Example 4.17

Two fair coins are tossed and the outcome is recorded.

  • A: Observe at least one head
  • B: Observe at least one tail

Define A, B, \(A \cup B\), \(A \cap B\), \(A^c\)

  • What are the events and what are the probabilities?

  • These concepts can be extended to more than two events (e.g. \(A \cup B \cup C\))

Calculating probabilities for Unions and Complements

  • The addition rule:

\[ P (A \cup B) = P(A) + P(B) - P(A \cap B) \]

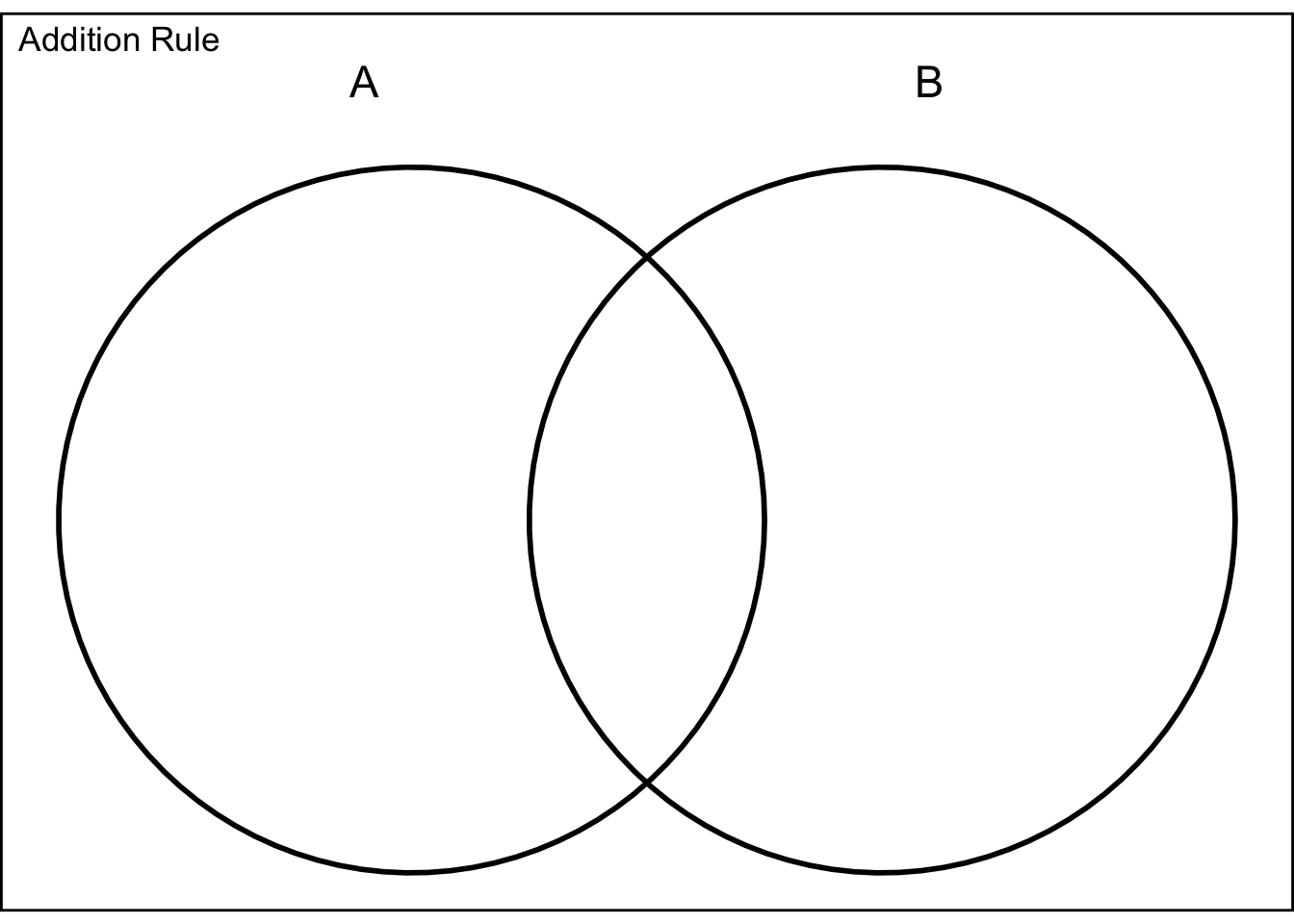
  • mutually exclusive: \(P(A \cap B) = 0\)

  • Rule for complements: \(P(A^c) = 1 - P(A)\)

Example 4.18

  • Drilling two exploratory wells:

  • A neither well produces oil or gas - 80%

  • B exactly one well produces oil or gas - 18%

  • C Both wells produce oil or gas - 2%

  • Find \(P(A \cup B)\) and \(P(B \cup C)\)

Calculating Probabilities for Intersections

  • Two events A and B are independent if and only if the probability of event B is not influenced or changed by the occurrence of event A or vice versa.

  • Color blindness/gender vs tossing a dice

  • General Multiplcation Rule

\[ P(A \cap B) = P(A)P(B|A) = P(B)P(A|B) \]

\(P(A|B)\) is read as probability of A given B - assuming B occurs. If the two events are independent then \(P(A|B) = P(A|B^c) = P(A)\)

Example 4.20

In a color preference experiment, eight toys are placed in a container. The toys are identical except fo color - two are red, and six are green. A child is asked to choose two toys at random. What is the probability that the child chooses the two red toys?

  • Use a tree diagram fo first and second choice
  • \(A = \text{(R on first choice) } \cap \text{ (R on second choice)}\)

Conditional Probabilities

The conditional probability of event A given that event B has occured is:

\[ P(A|B) = \frac{P(A\cap B)}{P(B)} \text{ if } P(B) \neq 0 \]

\[ P(B|A) = \frac{P(A\cap B)}{P(A)} \text{ if } P(A) \neq 0 \]

Colorblindness, continued

Men(\(B\)) Women(\(B^c\)) Total
Colorblind (\(A\)) .04 .002 .042
Not Colorblind (\(A^c\)) .47 .488 .958
Total .51 .49 1

  • If you pick a random person what is the chance they are colorblind?

  • If you pick a random male, what is the chance he is colorblind?

  • What is the chance a woman is?

The multiplication rule for independent events

If two events A and B are independent, the probability that both A and B occur is:

\[ P(A \cap B) = P(A)P(B) \]

Same thing for more than two events:

\[ P(A \cap B \cap C) = P(A)P(B)P(C) \]

Coin tosses In a Row

  • What the probability that the first toss is a heads, second toss is a tails, third toss is a heads?

  • What about all three tosses being heads?

Checking for independence

Two events are said to be independent if and only if either:

\[ P(A\cap B) = P(A)P(B) \]

or

\[ P(B|A) = P(B) \]

Example 4.22

Respondents were asked about the cost of a college education . The respondents were classified according to whether they currently had a chaild in college and whther they thought the loan burden for most college students is too high, the right amount or too little.

Too High (A) Right Amount (B) Too Little (C)
Child in College (D) .35 .08 .01
No Child in College (E) .25 .20 .11

Is A independent of D?

Also Remember the question about shooting free throw - is making the second one independent of making the first one?

Hit Second Miss Second
Hit First .49 .21
Miss First .21 .09

Mutually exclusive vs Independent

Homework

[1] "4.4.1, 4.4.7-4.4.10, 4.4.14, 4.4.27, 4.4.29,4.4.32, 4.4.35"

Answers: Chapter 4 - Section 4