Midterm Review 01

Chapter 01

1.4.21, 1.4.22, 1.4.25

Section 1.4

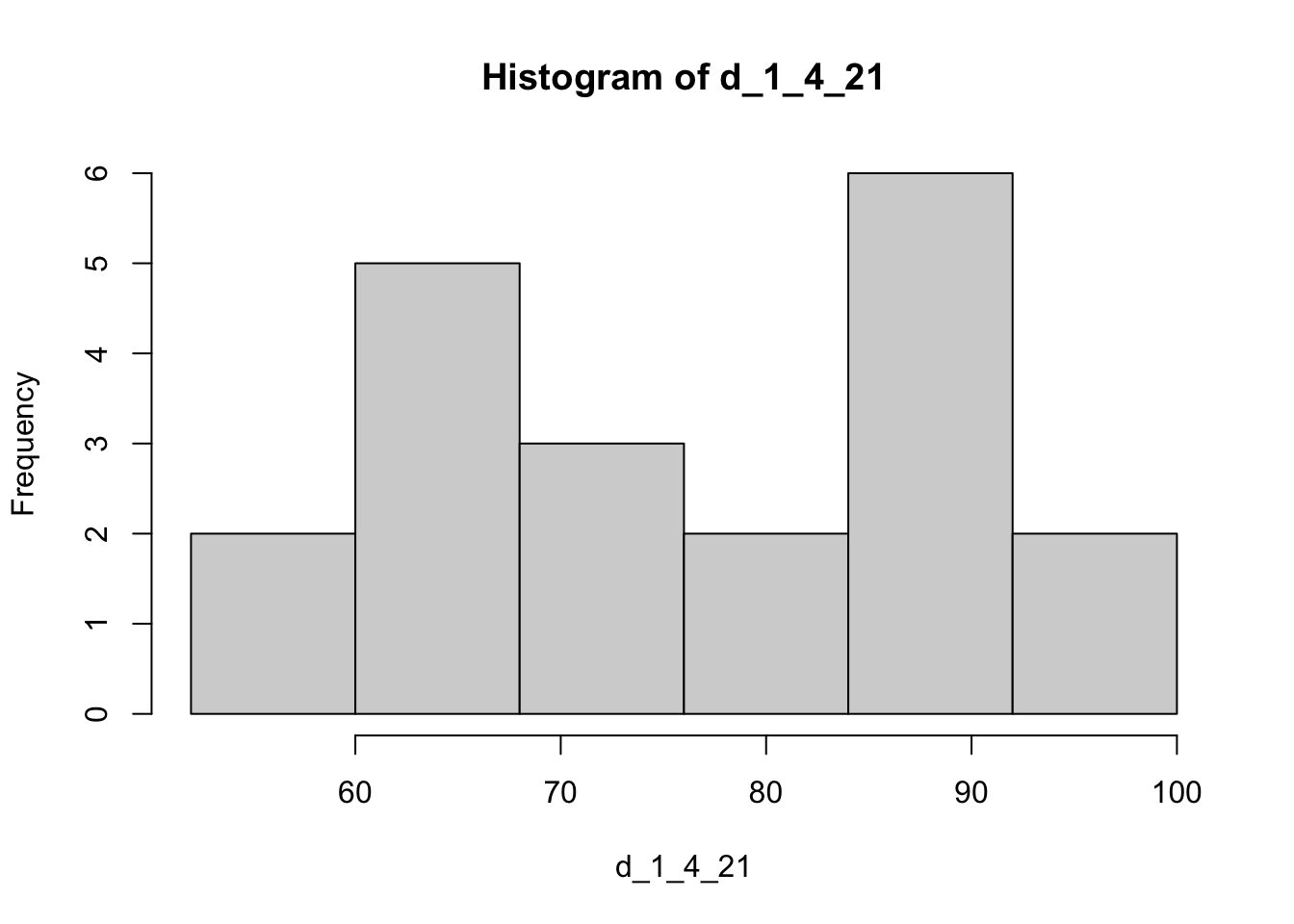
Q21 -Q 22

Has two peaks, one at about 65 and one at about 90
A bimodal shape is not usual. This could be because of two different classes that are differently prepared for the test.

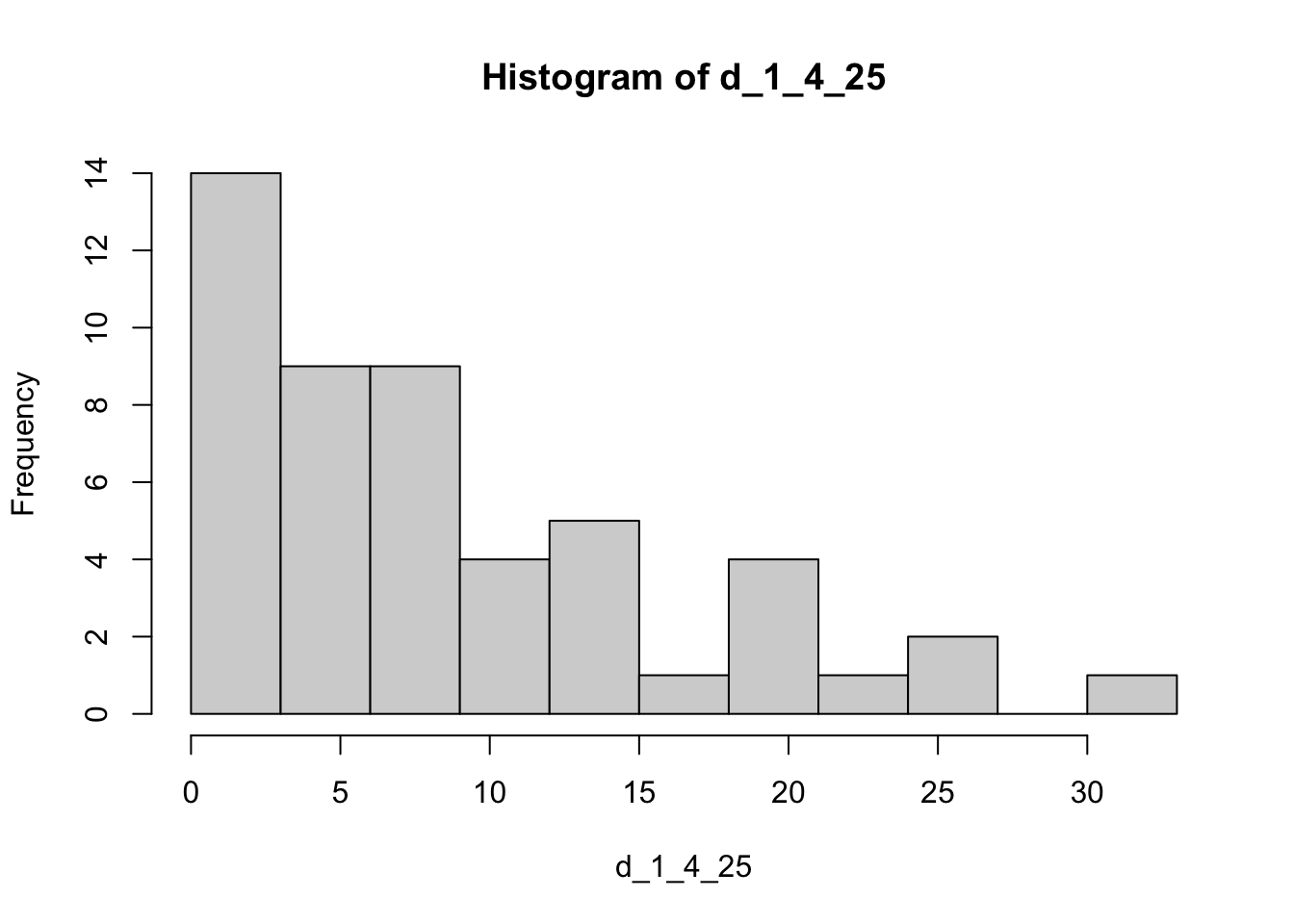
Q25

Min, max:

[1] 0.2

[1] 32.3

Range:

[1] 32.1

Let’s use 11 classes of width 3

	interval_start	interval_end	count	frequency
1	0	3	14	0.0933
2	3	6	9	0.0600
3	6	9	9	0.0600
4	9	12	4	0.0267
5	12	15	5	0.0333
6	15	18	1	0.0067
7	18	21	4	0.0267
8	21	24	1	0.0067
9	24	27	2	0.0133
10	27	30	0	0.0000
11	30	33	1	0.0067

Chapter 02

2.1.4, 2.1.9, 2.1.21
2.2.10
2.3.1, 2.3.6-14, 2.3.27

Section 01

Q4

Mean:

[1] 3.285714

Median:

[1] 3

Mode:

[1] "3"

Q9

Mean:

[1] 3.929167

Median:

[1] 3.9

Dataset looks fairly symmetric, mean and median are very close to each other.

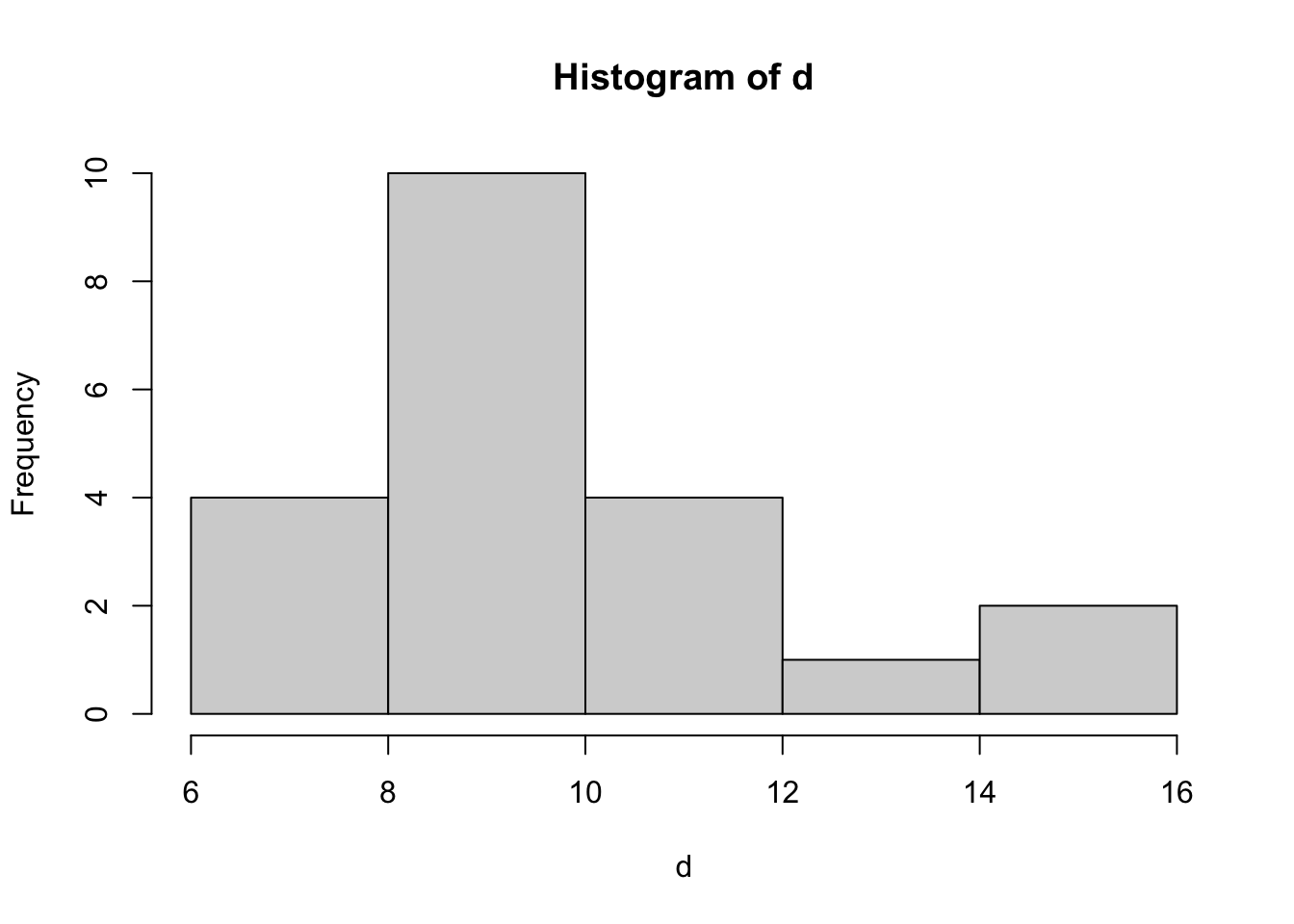
Q21

Mean:

[1] 9.690476

Median:

[1] 9.2

Mode:

[1] "6.8"  "8.2"  "10"   "10.4"

Data may be a little right skewed since the mean is to the right of the median.

Histogram (or dot plot) supports this statement

Section 2.2

Q10

Range:

[1] 1.11

Sample Variance:

[1] 0.19007

Sample Standard Deviation:

[1] 0.4359702

Mean:

[1] 1.712

The various pieces of the sample variance formula:

x	x - xbar	(x - xbar)^2
1.28	-0.432	0.186624
2.39	0.678	0.459684
1.50	-0.212	0.044944
1.88	0.168	0.028224
1.51	-0.202	0.040804

Range/SD:

[1] 2.546046

Range should be 4 x standard deviation, but it’s about 2.5. Not a perfect approximation but not too suprising since there are only 5 data apoints.

Section 2.3

Q1

Range:

[1] 5

Range approx of Std. Dev

[1] 1.25

Std. Dev:

[1] 1.75119

Pretty good approximation!

Q6 - Q11

k = 1, total = 68%
k = 2, total = 95%
between 30 and 50 = 95/2 = 47.5%, between 50 and 60 = 68/2 = 34%, total = 47.5 + 34 = 81.5%
< 50 = 50%. 50 to 60 = 34% (see number 8), Greater than 60 = 100% - 34% - 50% = 16%.
Less than 60: 100% - 16% = 84%
40 or more: 40 to 50 = 34%, greater than 50 = 50%, therefore 40 or more: 34 + 50 = 84%

Q12 - Q14

k = 3, At least 0.8888889
k = 2, At least 0.75
k = 2.5, At least 0.84

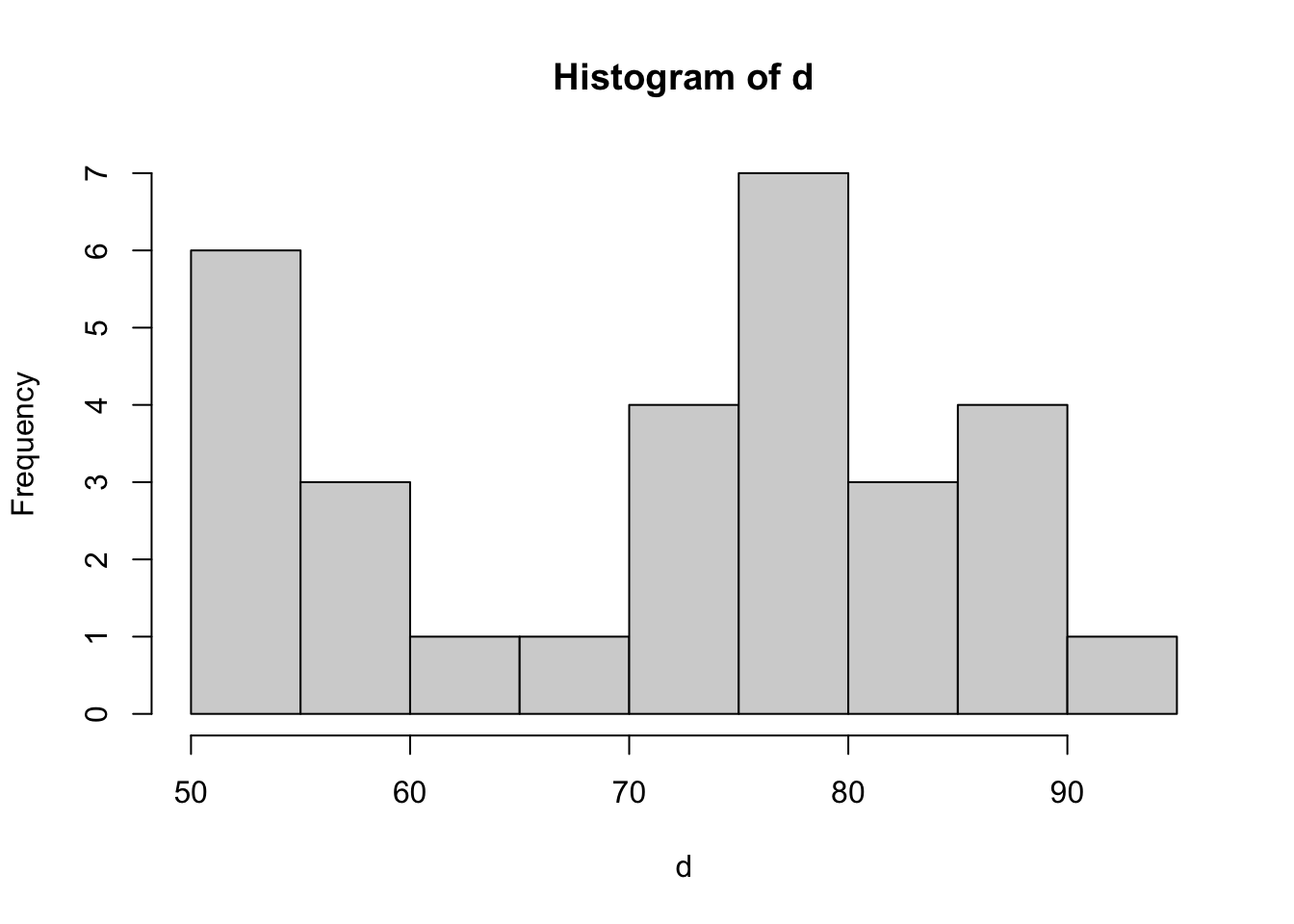
Q27

Range:

[1] 42

Range Approximatino of SD

[1] 10.5

Actual SD:

[1] 13.10107

Within 1 SD:

[1] 0.5333333

Within 2 sds:

[1] 1

Within 3 sds:

[1] 1

The empirical rule isn’t very accurate here - most likely to do the fact that the data is not mound shaped at all:

Chapter 04

4.1.13-15
4.2.11-15, 4.2.38, 4.2.40,
4.3.20, 4.3.25
4.4.16-18, 4.4.30, 4.4.36
4.5.7, 4.5.15

Section 1

Q13-Q15

See notes from class PDF of Notes

Section 2

Q11-Q15

E1 = E2 = .15, E3 = .4

E4 = 2E5

E1 + E2 + E3 + 2E5 + E5 = 1

.15 + .15 + .4 + 3E5 = 1

E5 = .1

E4 = .2
.15 + .4 + .2 = .75
.15 + .4 = .55
P(E1, E2, E3, E4) = 0.9
1 - .75 = .25

Q38

1 * 1/4 * 1/4 = 1/16 = 4 * (1/4 * 1/4 * 1/4)

Q40

a. 114/220

b. 25/220

c. 156/220

Section 3

Q20

2 * 2 * 2 = 8

Q25

a. 6 * 6 = 36

b. 1/6 * 1/6 = 1/36

c. 5/6

Section 4

Q16-17

Q16: a. 0, b. .8
Q17: a. .12/.4 = .3, b. no, c. Yes, P(B|A) = P(B)

Q18

a. 1
b. 1
c. 2/6
d. 0
e. 2/6
f. 0
g. 0
h. 1
i. 5/6

Q30

A - miss by first inspector

B - miss by second inspector

given: P(A) = .1, P(B|A) = 5/10 = .5

Question is asking for A and B to be true

Use multiplication rule:

\(P(A \cap B) = P(A)P(B|A) = .1 * .5 = .05\)

Q36

a. .71

b. .29

c. .35/.55

d. .36/.45

e. .35/.71

f. .09/.29

Section 5

Q7

\[ \begin{aligned} P(A) &= P(A|B)P(A) + P(A|B^c)P(B^c) \\ &= .6 * .3 + .5 * .4 \\ &= 0.38 \end{aligned} \]

Q15

\[ \begin{aligned} P(D) &= .1 \\ P(D^c) &= .9 \\ P(N|D^c) &= .85/.9 = .94\\ P(N|D) &= .02/.1 = .2 \end{aligned} \]

\[ \begin{aligned} P(D|N) & = \frac{P(N|D) P(D)}{P(N)} \\ &= \frac{P(N|D) P(D)}{P(N|D) P(D) + P(N|D^c) P(D^c)} \\ & = \frac{.2 *.1 }{.2 *.1 + .94* .9} \\ & = 0.023 \end{aligned} \]

Same as B but

\[ P(D|N) = P(D \cap N)/P(N) = .02 / .87 = .023 \]

d. \(P(P|D^c) = .05/.9 = 0.056\)

e. \(P(N|D) = .02/.1 = .2\)

f. The 20% false negative rate is a little high - it would miss 20% of disease.